Utilisation d’une thermistance NTC en capteur de température

Je m’étais promis de commencer à rédiger sur mes bricoles électroniques, c’est donc chose faite avec ce premier article qui a pour but de vous expliquer comment réaliser simplement un capteur de température. Étant donné que je fait beaucoup plus d’électronique que d’informatique sur mon temps libre en cette période, ça ne sera que positif pour ajouter du contenu par ici.

Cet article est le premier contenant quelques formules et développements, mais ne fuyez pas, le tout reste à la portée de tout élève ayant un niveau de terminale générale en maths (logarithmes, factorisation, …).

La thermistance NTC

Définition

Une thermistance (ou thermistor, version anglaise dérivée de resistor) est un composant passif qui a pour caractéristique de voir sa résistance varier en fonction de la température à laquelle elle est exposée.

On rencontre différents types de thermistances avec différentes courbes de variation température/résistance ; nous allons ici uniquement nous intéresser aux thermistances de type NTC (Negative Temperature Coefficient).

Les thermistances chinoises que j’ai trouvé sur eBay

Elles sont définies par plusieurs caractéristiques, parmis lesquelles :

$β$ une constante de température, en kelvins (K)
$R_{0}$ une résistance de référence, en ohms ( $Ω$ )
$T_{0}$ la température à laquelle s’applique la résistance de référence, en kevlins (K)

La relation entre sa résistance et la température est donnée par par la relation de Steinhart-Hart (merci Wikipédia) restreinte dans un domaine de température :

\begin{matrix} \frac{R_{t}}{R_{0}} = exp (β (\frac{1}{T} - \frac{1}{T_{0}})) \end{matrix}

Température en fonction de la résistance

On cherche à extraire $T$ de cette formule pour avoir la température :

\begin{matrix} \frac{ln (\frac{R_{T}}{R_{0}})}{β} = \frac{1}{T} - \frac{1}{T_{0}} \end{matrix}

\begin{matrix} \frac{ln (\frac{R_{T}}{R_{0}})}{β} + \frac{1}{T_{0}} = \frac{1}{T} \end{matrix}

D’où la relation suivante :

\begin{matrix} T (R_{T}) = \frac{1}{\frac{ln (\frac{R_{T}}{R_{0}})}{β} + \frac{1}{T_{0}}} \end{matrix}

Utilisation avec un pont diviseur de tension

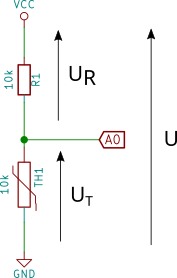
Une méthode simple en électronique pour mesurer facilement une variation de résistance d’un composant est de construire un pont diviseur de tension. Nous utiliserons donc notre thermistance ainsi qu’une autre résistance (de valeur égale à celle du $R_{0}$ de la thermistance, soit $10 k Ω$ pour les miennes) pour former le pont schématisé ci-dessous :

Schéma de notre pont diviseur de tension

Avec $U_{T}$ la tension aux bornes de la thermistance, $U_{R}$ la tension aux bornes de la résistance et $U$ la tension entre le haut et le bas du diviseur (typiquement VCC).

En appliquant la formule du pont diviseur de tension au niveau de $U_{T}$ , on obtient la relation suivante entre les différentes tensions du circuit :

\begin{matrix} U_{T} = U \frac{R_{T}}{R_{T} + R} \end{matrix}

Nous allons devoir manipuler la formule pour pouvoir retrouver $R_{T}$ en fonction des tensions présentes dans le circuit, ce qui va nous permettre par la suite de réinjecter cette formulation de $R_{T}$ dans la formule de calcul de la température pour directement obtenir la température à partir de la tension !

Voici le développement :

\begin{matrix} U_{T} = U \frac{R_{T}}{R_{T} + R} \end{matrix}

\begin{matrix} \frac{U_{T}}{U} = \frac{R_{T}}{R_{T} + R} \end{matrix}

\begin{matrix} \frac{U_{T}}{U} (R_{T} + R) = R_{T} \end{matrix}

\begin{matrix} \frac{U_{T}}{U} R_{T} + \frac{U_{T}}{U} R = R_{T} \end{matrix}

\begin{matrix} \frac{U_{T}}{U} R = R_{T} - \frac{U_{T}}{U} R_{T} \end{matrix}

\begin{matrix} \frac{U_{T}}{U} R = R_{T} (1 - \frac{U_{T}}{U}) \end{matrix}

\begin{matrix} \frac{\frac{U_{T}}{U} R}{1 - \frac{U_{T}}{U}} = R_{T} \end{matrix}

Et voilà, on peut maintenant retrouver la résistance en fonction de la tension $U_{T}$ que l’on va mesurer. En réinjectant cette définition de $R_{T}$ dans la formule de calcul de température, on obtient la (grosse) relation suivante :

\begin{matrix} T (U_{T}) = \frac{1}{\frac{ln \frac{(\frac{\frac{U_{T}}{U} R}{1 - \frac{U_{T}}{U}})}{R_{0}}}{β} + \frac{1}{T_{0}}} \end{matrix}

Voici des exemples d’applications numériques en considérant pour l’exemple une tension de référence $U = 5 V$ avec les caractéristiques de mes thermistances :

$T (1.5 V) = 321 K$ (soit 48 °C)
$T (2.5 V) = 298 K$ (soit 25 °C)
$T (3.5 V) = 278 K$ (soit 5 °C)

Avis

Courrier des lecteurs — 2019-09-24

Le développement ci-dessus est bien compliqué, car je suis parti bille en tête sur la formule du pont diviseur de tension. On peut cependant utiliser la loi d'Ohm, qui va nous donner une formule plus simple.

Prenons les deux applications suivantes de la loi d'Ohm à notre circuit :

\begin{matrix} U_{R} = R \cdot I \Rightarrow I = \frac{U_{R}}{R} \\ U_{T} = R_{T} \cdot I \Rightarrow I = \frac{U_{T}}{R_{T}} \end{matrix}

On peut donc arriver à l'égalité suivante :

\begin{matrix} \frac{U_{R}}{R} = \frac{U_{T}}{R_{T}} \end{matrix}

Cependant, cette formule n'est pas pratique car notre montage ne mesure pas $U_{R}$ mais seulement $U_{T}$ . On peut néanmoins déduire $U_{R}$ :

\begin{matrix} U_{R} = U - U_{T} \end{matrix}

Et donc on obtient :

\begin{matrix} \frac{U - U_{T}}{R} = \frac{U_{T}}{R_{T}} \\ R_{T} = \frac{U_{T} \cdot R}{U - U_{T}} \end{matrix}

Ce qui nous donne la formule finale suivante pour retouver la température :

\begin{matrix} T (U_{T}) = \frac{1}{\frac{ln \frac{(\frac{U_{T} \cdot R}{U - U_{T}})}{R_{0}}}{β} + \frac{1}{T_{0}}} \end{matrix}

Qui est plus simple que celle avec le pont diviseur de tension.

Merci à P. Loos pour cette astuce.

Plus qu’à tester en vrai

Pfiou, après les formules, on va enfin pouvoir passer au test grandeur nature !

Pour cela, nous allons devoir utiliser un ADC pour convertir la tension analogique que l’on mesure au milieu du diviseur de tension en une valeur numérique sur laquelle faire des calculs pour trouver la température.

Meet the BeagleBone Black

N’importe quel microcontrôleur pourrait faire l’affaire mais il faudrait gérer l’affichage derrière ou utiliser le port série avec une Arduino. C’est pour ça que j’ai sorti ma toute nouvelle BeagleBone Black, qui dispose également de plusieurs ADCs (à 1,8 V et non pas 5 V) dont on va pouvoir se servir.

Le montage de pont diviseur de tension relié à une entrée analogique de la carte

L’avantage est que je vais pouvoir directement effectuer les calculs sur la carte et les lire sur l’écran de mon PC en utilisant une connexion SSH par le câble USB (qui sert d’interface réseau ici). De plus, on a à notre disposition un système Linux complet, ce qui veut dire que l’on peut même programmer en Python dessus pour réaliser un prototype au lieu de se casser la tête avec du C (qui serait par contre obligatoire si on voudrait faire de l’acquisition haute fréquence).

Code d’acquisition et de conversion

J’ai donc réalisé un petit script Python qui va venir lire à une certaine fréquence la valeur lue par l’ADC de 2048 bits mise à disposition dans un fichier système par les pilotes de la carte.

Voici le code en question (en Python 2 car il était déjà installé avec la carte) :

# encoding: utf-8

from time import sleep
from math import log


# Calcule la température en degrés kevlin
def temp_kelvin(val):
        u = 1.8                  # Tension d’alimentation du pont diviseur
        r = 10000.0              # Résistance en haut du pont
        ut = val * u / 2048.0    # Tension mesurée avec l’entrée analogique
        beta = 3435.0            # Constante de la thermistance
        r0 = 10000.0             # Résistance de référence de la thermistance
        t0 = 298.0               # Température de référence
        return 1/((log(((ut*r/u)/(1-(ut/u)))/r0)/beta)+(1/t0)) - 5 # yolo calibration


# Calcule la température en degrés celcius
def temp(val):
        return temp_kelvin(val) - 273


# Boucle principale
while 1:
        # On réouvrre le fichier à chaque fois pour être sûr de lancer
        # l’acquisition
        with open('/sys/devices/ocp.3/helper.15/AIN0') as f:
                val = int(f.read())
                print "Temperature (°C)  {}:".format(temp(val))
        # On fait une petite pause pour ne pas spammer le terminal et le
        # processeur
        sleep(0.1)

Vous pouvez voir que j’ai rajouté un offset à la formule que nous avions trouvée car en effet j’avais une différence de 5 °C entre la température lue et celle des thermomètres numériques et à alcool que j’ai utilisé pour vérifier le résultat. Une fois cet offset ajouté, la valeur lue concorde avec les thermomètres à 1 °C près, ce qui n’est pas trop mal étant donné que le calcul d’erreur théorique − que je ne détaillerai pas ici − donnait une précision de 3 °C.

Avis

Courrier des lecteurs — 2019-09-24

Il est conseillé de mesurer la résistance R choisie (de préférence une résistance de précision), ainsi que le paramètre de la thermistance NTC $R_{0}$ à 25 °C — puis à 85 °C — plutôt que de se fier aux données du constructeur. Ces valeurs sont données à 10 % de précision pour les composants premier prix tel que ceux que j'utilise ici. Il est donc important de les mesurer.

Merci à P. Loos pour cette précision.

Cependant, je n’ai pas eu l’occasion de tester ce capteur de température dans des gammes éloignées des 20 °C de l’air ambiant ; je retesterai la formule cet hiver pour vérifier qu’elle n’est pas faussée, mais je suis plutôt confiant.

Et après ?

Je valide personnellement ce capteur de température à pas cher à base de thermistances chinoises et de pont diviseur de tension.

On peut donc envisager des applications plus avancées telles qu’un réseau de capteurs pour vérifier la température dans différentes pièces d’une maison, ou bien un petit traqueur de température autonome à base de microcontrôleur qui réalise des mesures à intervalle régulier dans une EEPROM que l’on peut ensuite lire pour voir les variations pendant une journée complète par exemple.

Pour les plus motivés pourquoi pas réaliser une interface web HTML5 qui permettrai de consulter cette température et son évolution à distance en routant correctement sa box.

Conclusion

Ce montage a été amusant à réaliser et j’ai enfin un capteur intéressant à exploiter avec ma BeagleBone ou les microcontrôleurs qui trainent dans mes tiroirs.

Vous pouvez vous aussi réaliser vos propres capteurs en suivant ce principe, par contre je ne garantie pas la fiabilité par rapport à des sondes de températures un peu plus chères mais sans doute beaucoup plus précises.